Aditya Dendukuri

Github

About Me & Research Interests
I'm a computational scientist at the intersection of applied mathematics, scientific computing, and data science. My work focuses on stochastic modeling of discrete systems, rare event sampling methods, and efficient algorithms for high-dimensional systems. I enjoy collaborating across scientific disciplines, incorporating both computational and mathematical approaches to solve complex problems.

Current Projects
1. Efficient Stochastic Simulation Methods for Discrete Systems
I develop algorithms for simulating stochastic biochemical networks governed by the Chemical Master Equation:

$$ \frac{dP(\mathbf{x},t)}{dt} = \sum_{\mathbf{x}'\neq\mathbf{x}} \Bigl[W_{\mathbf{x}'\to\mathbf{x}}\,P(\mathbf{x}',t) - W_{\mathbf{x}\to\mathbf{x}'}\,P(\mathbf{x},t)\Bigr] $$

My research focuses on controlling the finite state space of these systems over time. For example, in genetic toggle switches (two mutually repressing genes), reactions include:

$$ \varnothing \xrightarrow{\frac{\beta_A}{1+(B/K_B)^{n_B}}} A,\; A \xrightarrow{\delta_A} \varnothing \quad \text{and} \quad \varnothing \xrightarrow{\frac{\beta_B}{1+(A/K_A)^{n_A}}} B,\; B \xrightarrow{\delta_B} \varnothing $$

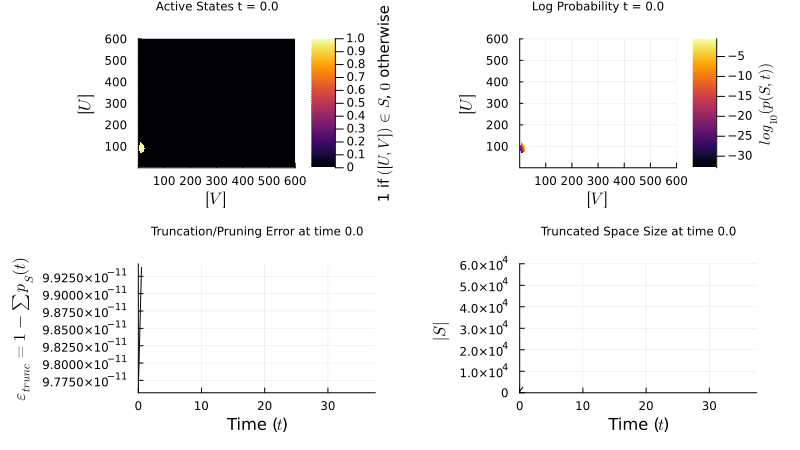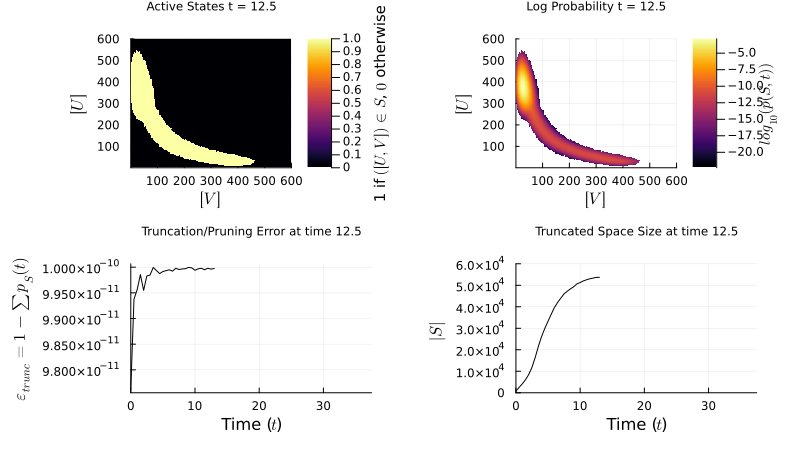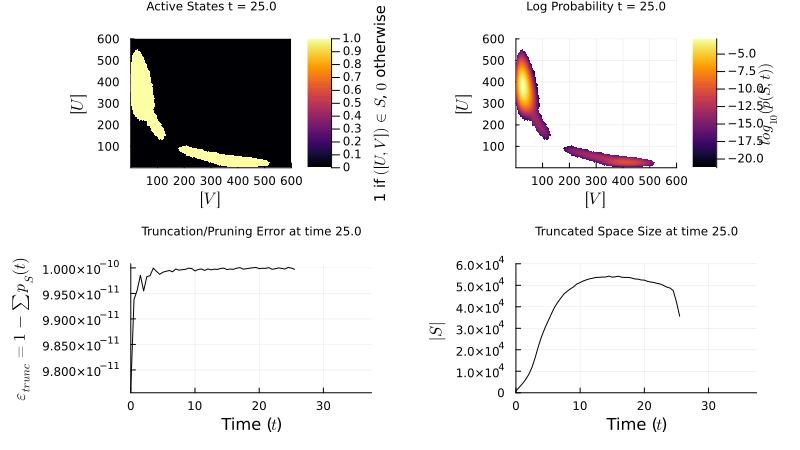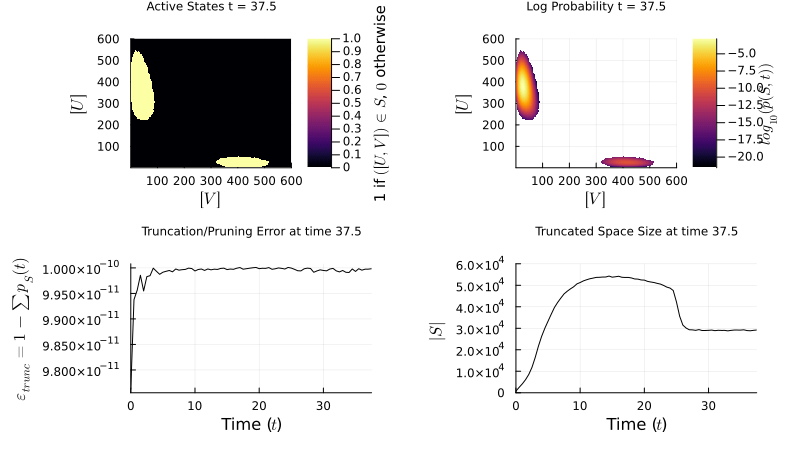I implement the Finite State Projection (FSP) method to manage large state spaces:

$$ \mathbf{W} = \begin{pmatrix} \mathbf{Q} & \mathbf{R} \\ \mathbf{T} & \mathbf{U} \end{pmatrix} \quad \text{approximated by} \quad \widetilde{\mathbf{W}} = \begin{pmatrix} \mathbf{Q} & \mathbf{R} \\ \mathbf{0} & \mathbf{0} \end{pmatrix} $$

2. Markov Simulation of Nucleation (Crystal Formation)
I developed Monte Carlo simulations of the Ising model to study nucleation—the initial stage of phase transitions such as crystallization. This C-based implementation applies umbrella sampling to construct free energy landscapes and capture rare nucleation events. The simulation is validated against theoretical predictions and includes visualization through ffmpeg integration.

GitHub Repository