Aditya Dendukuri

Github

About Me & Research Interests
My research lies at the intersection of applied mathematics, scientific computing, and data science, with a focus on stochastic modeling of discrete systems, rare-event sampling, and scalable algorithms for high-dimensional problems. I am particularly motivated by interdisciplinary collaboration and enjoy combining rigorous mathematical analysis with modern computational methods to tackle challenging scientific questions.

Current Projects
1. Efficient Stochastic Simulation Methods for Discrete Systems
I develop algorithms for simulating stochastic biochemical networks governed by the Chemical Master Equation:

$$ \frac{dP(\mathbf{x},t)}{dt} = \sum_{\mathbf{x}'\neq\mathbf{x}} \Bigl[W_{\mathbf{x}'\to\mathbf{x}}\,P(\mathbf{x}',t) - W_{\mathbf{x}\to\mathbf{x}'}\,P(\mathbf{x},t)\Bigr] $$

My research focuses on controlling the finite state space of these systems over time. For example, in genetic toggle switches (two mutually repressing genes), reactions include:

$$ \varnothing \xrightarrow{\frac{\beta_A}{1+(B/K_B)^{n_B}}} A,\; A \xrightarrow{\delta_A} \varnothing \quad \text{and} \quad \varnothing \xrightarrow{\frac{\beta_B}{1+(A/K_A)^{n_A}}} B,\; B \xrightarrow{\delta_B} \varnothing $$

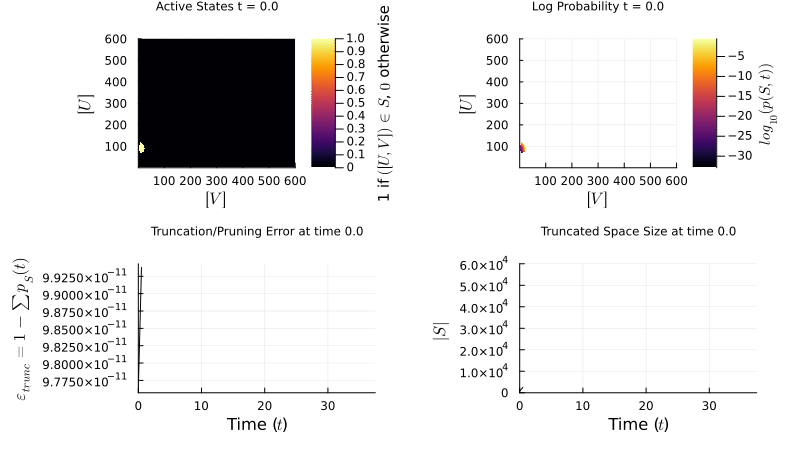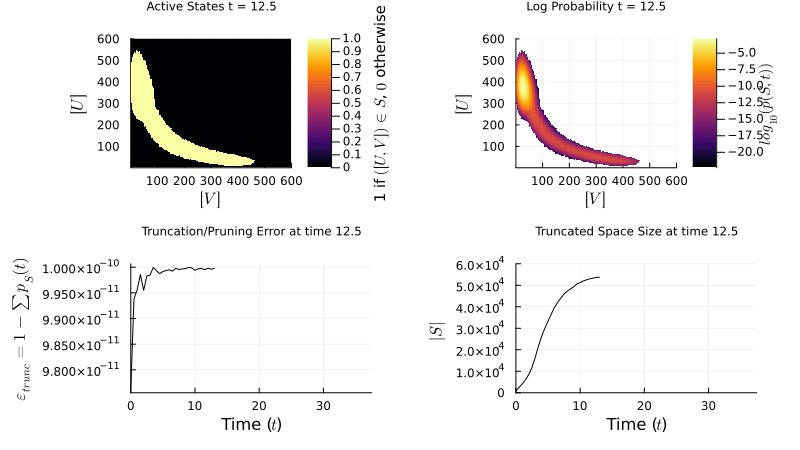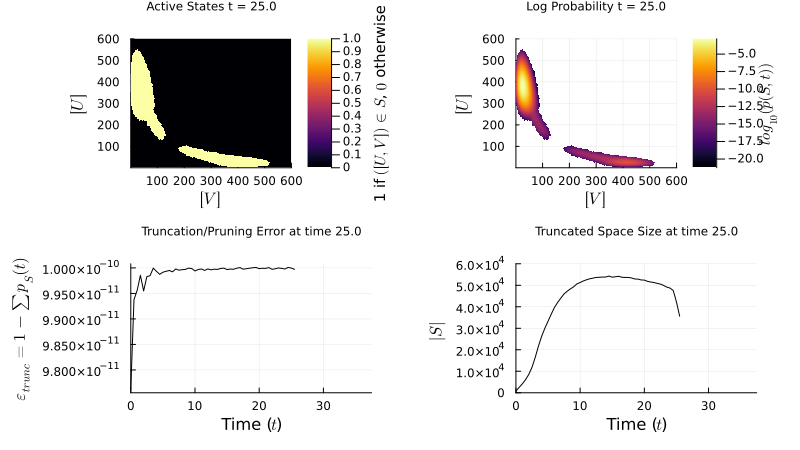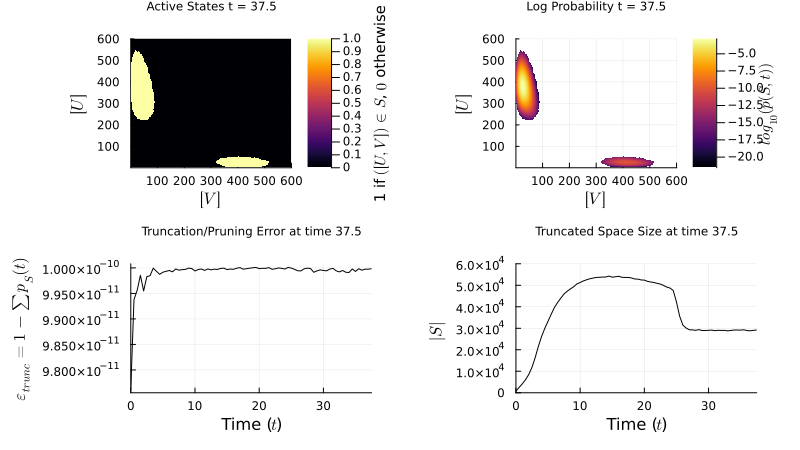I implement the Finite State Projection (FSP) method to manage large state spaces:

$$ \mathbf{W} = \begin{pmatrix} \mathbf{Q} & \mathbf{R} \\ \mathbf{T} & \mathbf{U} \end{pmatrix} \quad \text{approximated by} \quad \widetilde{\mathbf{W}} = \begin{pmatrix} \mathbf{Q} & \mathbf{R} \\ \mathbf{0} & \mathbf{0} \end{pmatrix} $$

2. Markov Simulation of Nucleation (Crystal Formation)
I developed Monte Carlo simulations of the Ising model to study nucleation—the initial stage of phase transitions such as crystallization. This C-based implementation applies umbrella sampling to construct free energy landscapes and capture rare nucleation events. The simulation is validated against theoretical predictions and includes visualization through ffmpeg integration.

GitHub Repository